–°—А–Њ—З–љ–∞—П –њ—Г–±–ї–Є–Ї–∞—Ж–Є—П –љ–∞—Г—З–љ–Њ–є —Б—В–∞—В—М–Є
+7 995 770 98 40
+7 995 202 54 42
info@journalpro.ru
–Ю—Б–Њ–±–µ–љ–љ–Њ—Б—В–Є —Д–Њ—А–Љ–Є—А–Њ–≤–∞–љ–Є—П –≤—Л—З–Є—Б–ї–Є—В–µ–ї—М–љ—Л—Е –љ–∞–≤—Л–Ї–Њ–≤ —Г —Б–ї–∞–±–Њ—Г—Б–њ–µ–≤–∞—О—Й–Є—Е —Г—З–µ–љ–Є–Ї–Њ–≤
–†—Г–±—А–Є–Ї–∞: –Я–µ–і–∞–≥–Њ–≥–Є—З–µ—Б–Ї–Є–µ –љ–∞—Г–Ї–Є
–Ц—Г—А–љ–∞–ї: «–Х–≤—А–∞–Ј–Є–є—Б–Ї–Є–є –Э–∞—Г—З–љ—Л–є –Ц—Г—А–љ–∞–ї вДЦ1 2018» (—П–љ–≤–∞—А—М, 2018)
–Ъ–Њ–ї–Є—З–µ—Б—В–≤–Њ –њ—А–Њ—Б–Љ–Њ—В—А–Њ–≤ —Б—В–∞—В—М–Є: 1428
–Я–Њ–Ї–∞–Ј–∞—В—М PDF –≤–µ—А—Б–Є—О –Ю—Б–Њ–±–µ–љ–љ–Њ—Б—В–Є —Д–Њ—А–Љ–Є—А–Њ–≤–∞–љ–Є—П –≤—Л—З–Є—Б–ї–Є—В–µ–ї—М–љ—Л—Е –љ–∞–≤—Л–Ї–Њ–≤ —Г —Б–ї–∞–±–Њ—Г—Б–њ–µ–≤–∞—О—Й–Є—Е —Г—З–µ–љ–Є–Ї–Њ–≤
–Ъ—А—О—З–Ї–Њ–≤–∞ –°–≤–µ—В–ї–∞–љ–∞ –Э–Є–Ї–Њ–ї–∞–µ–≤–љ–∞
–Я—А–Є –Њ–±—Г—З–µ–љ–Є–Є –Љ–∞—В–µ–Љ–∞—В–Є–Ї–µ —Б–ї–∞–±–Њ—Г—Б–њ–µ–≤–∞—О—Й–Є—Е –і–µ—В–µ–є, –≤–Њ–Ј–љ–Є–Ї–∞–µ—В –њ–Њ—В—А–µ–±–љ–Њ—Б—В—М —Г–њ—А–Њ—Й–µ–љ–Є—П –Љ–µ—В–Њ–і–Њ–≤ —А–µ—И–µ–љ–Є—П –Ј–∞–і–∞—З. –Э—Г–ґ–љ—Л –Љ–µ—В–Њ–і—Л, –њ—Г—Б—В—М –њ–Њ—А–Њ–є –Є –љ–µ —Б–∞–Љ—Л–µ —А–∞—Ж–Є–Њ–љ–∞–ї—М–љ—Л–µ, –љ–Њ –ї—С–≥–Ї–Є–µ –≤ —Г—Б–≤–Њ–µ–љ–Є–Є –Є –і–∞—О—Й–Є–µ –≥–∞—А–∞–љ—В–Є—А–Њ–≤–∞–љ–љ—Л–є —А–µ–Ј—Г–ї—М—В–∞—В –≤ —А–µ—И–µ–љ–Є–Є –Ј–∞–і–∞–љ–Є—П.
–Ш–Ј–≤–ї–µ—З–µ–љ–Є–µ –Ї–≤–∞–і—А–∞—В–љ–Њ–≥–Њ –Ї–Њ—А–љ—П –Ј–∞—З–∞—Б—В—Г—О –≤—Л–Ј—Л–≤–∞–µ—В –Ј–∞—В—А—Г–і–љ–µ–љ–Є–µ —Г –Љ–љ–Њ–≥–Є—Е —Г—З–∞—Й–Є—Е—Б—П, –Њ—Б–Њ–±–µ–љ–љ–Њ –µ—Б–ї–Є –љ—Г–ґ–љ–Њ –Є–Ј–≤–ї–µ—З—М –Ї–≤–∞–і—А–∞—В–љ—Л–є –Ї–Њ—А–µ–љ—М –Є–Ј —В—А—С—Е–Ј–љ–∞—З–љ–Њ–≥–Њ —З–Є—Б–ї–∞ –±–µ–Ј —В–∞–±–ї–Є—Ж—Л –Ї–≤–∞–і—А–∞—В–Њ–≤.
–Т —В–∞–Ї–Є—Е —Б–ї—Г—З–∞—П—Е —П –њ—А–µ–і–ї–∞–≥–∞—О —Г—З–∞—Й–Є–Љ—Б—П –і–µ–є—Б—В–≤–Њ–≤–∞—В—М —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ: –І–Є—Б–ї–Њ –њ–Њ–і –Ї–Њ—А–љ–µ–Љ —А–∞—Б–Ї–ї–∞–і—Л–≤–∞–µ—В—Б—П –љ–∞ –Љ–љ–Њ–ґ–Є—В–µ–ї–Є. –Ъ–∞–Ї —В–Њ–ї—М–Ї–Њ –≤ –њ–Њ–і–Ї–Њ—А–µ–љ–љ–Њ–Љ –≤—Л—А–∞–ґ–µ–љ–Є–Є –њ–Њ—П–≤–ї—П–µ—В—Б—П –і–≤–∞ –Њ–і–Є–љ–∞–Ї–Њ–≤—Л—Е –Љ–љ–Њ–ґ–Є—В–µ–ї—П вАФ –Є—Е –Ј–∞—З—С—А–Ї–Є–≤–∞—О—В –Є –Њ–і–Є–љ –Ј–∞–њ–Є—Б—Л–≤–∞—О—В –њ–µ—А–µ–і –Ј–љ–∞–Ї–Њ–Љ –Ї–Њ—А–љ—П. –Ґ–∞–Ї –і–µ–є—Б—В–≤—Г—О—В –і–Њ —В–µ—Е –њ–Њ—А, –њ–Њ–Ї–∞ —З–Є—Б–ї–Њ –њ–Њ–і –Ї–Њ—А–љ–µ–Љ –љ–µ —Б—В–∞–љ–µ—В –њ—А–Њ—Б—В—Л–Љ.
–Э–∞–њ—А–Є–Љ–µ—А
![]()
–Я–Њ—А–Њ–є –і–µ—В–Є –љ–µ —Б—А–∞–Ј—Г –≤–Є–і—П—В –љ–∞–Є–±–Њ–ї–µ–µ –њ—А–Њ—Б—В–Њ–є –њ—Г—В—М —А–∞–Ј–ї–Њ–ґ–µ–љ–Є—П –љ–∞ –Љ–љ–Њ–ґ–Є—В–µ–ї–Є, –Є—Е –љ–µ –љ—Г–ґ–љ–Њ –Њ—Б—В–∞–љ–∞–≤–ї–Є–≤–∞—В—М –Є –њ–Њ–њ—А–∞–≤–ї—П—В—М, –≥–ї–∞–≤–љ–Њ–µ, —З—В–Њ–±—Л –Њ–љ–Є –Ї–∞–ґ–і—Л–Љ —И–∞–≥–Њ–Љ —А–∞—Б–Ї–ї–∞–і—Л–≤–∞–ї–Є –љ–∞ –Љ–љ–Њ–ґ–Є—В–µ–ї–Є –Њ–і–љ–Њ –Є–Ј —З–Є—Б–µ–ї –њ–Њ–і –Ї–Њ—А–љ–µ–Љ –Є –њ–Њ—Б–ї–µ –Ї–∞–ґ–і–Њ–≥–Њ —Н—В–∞–њ–∞ –њ—А–Њ–≤–µ—А—П–ї–Є –љ–∞ –њ–Њ—П–≤–ї–µ–љ–Є–µ –і–≤—Г—Е –Њ–і–Є–љ–∞–Ї–Њ–≤—Л—Е –Љ–љ–Њ–ґ–Є—В–µ–ї–µ–є. –Ґ–∞–Ї–Є–Љ —Б–њ–Њ—Б–Њ–±–Њ–Љ –і–∞–ґ–µ —Б–ї–∞–±–Њ—Г—Б–њ–µ–≤–∞—О—Й–Є–µ —Г—З–µ–љ–Є–Ї–Є —Г—Б–њ–µ—И–љ–Њ –Є–Ј–≤–ї–µ–Ї–∞—О—В –Ї–≤–∞–і—А–∞—В–љ—Л–є –Ї–Њ—А–µ–љ—М –Є–Ј –±–Њ–ї—М—И–Є—Е —З–Є—Б–µ–ї.
–Э–∞–њ—А–Є–Љ–µ—А, —Б —В–∞–Ї–Є–Љ –Ј–∞–і–∞–љ–Є–µ–Љ –Є–Ј —Б–±–Њ—А–љ–Є–Ї–∞ –њ–Њ –њ–Њ–і–≥–Њ—В–Њ–≤–Ї–µ –Ї –Ю–У–≠
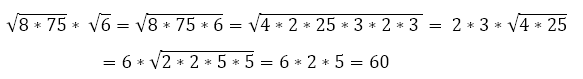
–Њ–њ–Є—Б–∞–љ–љ—Л–Љ –Љ–µ—В–Њ–і–Њ–Љ —Г—Б–њ–µ—И–љ–Њ —Б–њ—А–∞–≤–ї—П–µ—В—Б—П –±–Њ–ї—М—И–Є–љ—Б—В–≤–Њ —Б–ї–∞–±–Њ—Г—Б–њ–µ–≤–∞—О—Й–Є—Е —Г—З–µ–љ–Є–Ї–Њ–≤, —А–∞–љ–µ–µ –Є—Б–њ—Л—В—Л–≤–∞–≤—И–Є—Е —Б–µ—А—М—С–Ј–љ—Л–µ –Ј–∞—В—А—Г–і–љ–µ–љ–Є—П –њ—А–Є –Є–Ј–≤–ї–µ—З–µ–љ–Є–Є –Ї–≤–∞–і—А–∞—В–љ–Њ–≥–Њ –Ї–Њ—А–љ—П –і–∞–ґ–µ –Є–Ј –±–Њ–ї–µ–µ –њ—А–Њ—Б—В—Л—Е —З–Є—Б–µ–ї.
–Я—А–Є –њ—А–Є–≤–µ–і–µ–љ–Є–Є –Њ–±—Л–Ї–љ–Њ–≤–µ–љ–љ—Л—Е –і—А–Њ–±–µ–є –Ї –Њ–±—Й–µ–Љ—Г –Ј–љ–∞–Љ–µ–љ–∞—В–µ–ї—О, –љ–µ–Ї–Њ—В–Њ—А—Л–µ —Г—З–∞—Й–Є–µ—Б—П –љ–µ –Љ–Њ–≥—Г—В —Г—Б–≤–Њ–Є—В—М –Љ–µ—В–Њ–і–Њ–≤ –љ–∞—Е–Њ–ґ–і–µ–љ–Є—П –Э–Ю–Ф –Є –њ–Њ–њ—А–Њ—Б—В—Г –Є—Б–њ–Њ–ї—М–Ј—Г—О—В –Ј–љ–∞–Љ–µ–љ–∞—В–µ–ї–Є –і—А–Њ–±–µ–є –Ї–∞–Ї –і–Њ–њ–Њ–ї–љ–Є—В–µ–ї—М–љ—Л–µ –Љ–љ–Њ–ґ–Є—В–µ–ї–Є ¬Ђ–Ї—А–µ—Б—В-–љ–∞–Ї—А–µ—Б—В¬ї —Г–Љ–љ–Њ–ґ–∞—П –±–Њ–ї—М—И–Є–µ —З–Є—Б–ї–∞ –Є –і–Њ–њ—Г—Б–Ї–∞—П –≤—Л—З–Є—Б–ї–Є—В–µ–ї—М–љ—Л–µ –Њ—И–Є–±–Ї–Є. –Ф–ї—П —В–∞–Ї–Є—Е —Б–ї—Г—З–∞–µ–≤ –Љ–љ–Њ—О –њ—А–µ–і–ї–∞–≥–∞–µ—В—Б—П —Б–ї–µ–і—Г—О—Й–Є–є —Б–њ–Њ—Б–Њ–± –љ–∞—Е–Њ–ґ–і–µ–љ–Є—П –і–Њ–њ–Њ–ї–љ–Є—В–µ–ї—М–љ—Л—Е –Љ–љ–Њ–ґ–Є—В–µ–ї–µ–є: –Ч–љ–∞–Љ–µ–љ–∞—В–µ–ї–Є –і—А–Њ–±–µ–є –њ–Њ–і–њ–Є—Б—Л–≤–∞—О—В—Б—П –Ї–∞–Ї –і–Њ–њ–Њ–ї–љ–Є—В–µ–ї—М–љ—Л–µ –Љ–љ–Њ–ґ–Є—В–µ–ї–Є ¬Ђ–Ї—А–µ—Б—В-–љ–∞–Ї—А–µ—Б—В¬ї –Є –Ј–∞—В–µ–Љ —Г—З–∞—Й–Є–Љ—Б—П –њ—А–µ–і–ї–∞–≥–∞–µ—В—Б—П –Њ–њ—А–µ–і–µ–ї–Є—В—М вАФ –Љ–Њ–ґ–љ–Њ –ї–Є —Б–Њ–Ї—А–∞—В–Є—В—М —Н—В–Є –Љ–љ–Њ–ґ–Є—В–µ–ї–Є –љ–∞ –Ї–∞–Ї–Њ–µ-–ї–Є–±–Њ —З–Є—Б–ї–Њ. –° —Н—В–Є–Љ –≤–Њ–њ—А–Њ—Б–Њ–Љ —Г—З–∞—Й–Є–µ—Б—П –Ї–∞–Ї –њ—А–∞–≤–Є–ї–Њ —Б–њ—А–∞–≤–ї—П—О—В—Б—П —Г—Б–њ–µ—И–љ–Њ –Є —Б–Њ–Ї—А–∞—Й–∞—О—В –Љ–љ–Њ–ґ–Є—В–µ–ї–Є.
–Э–∞–њ—А–Є–Љ–µ—А,
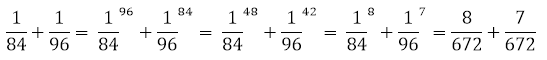
–£—З–∞—Й–Є–µ—Б—П —Б–Њ–Ї—А–∞—Й–∞—О—В –і–Њ–њ–Њ–ї–љ–Є—В–µ–ї—М–љ—Л–µ –Љ–љ–Њ–ґ–Є—В–µ–ї–Є –љ–∞ 2, –Ј–∞—В–µ–Љ –љ–∞ 6. –Ґ–µ, –Ї—В–Њ –Ј–∞–±—Л–ї–Є —В–∞–±–ї–Є—Ж—Г —Г–Љ–љ–Њ–ґ–µ–љ–Є—П –Є ¬Ђ–љ–µ –≤–Є–і—П—В¬ї, —З—В–Њ –Љ–Њ–ґ–љ–Њ —Б–Њ–Ї—А–∞—В–Є—В—М –љ–∞ 6, –µ—Й—С —А–∞–Ј —Б–Њ–Ї—А–∞—Й–∞—О—В –љ–∞ 2, –Ј–∞—В–µ–Љ –љ–∞ 3. –Ш —В–∞–Ї –і–Њ —В–µ—Е –њ–Њ—А, –њ–Њ–Ї–∞ –Є–Љ–µ–µ—В—Б—П –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ—Б—В—М —Б–Њ–Ї—А–∞—В–Є—В—М –і–Њ–њ–Њ–ї–љ–Є—В–µ–ї—М–љ—Л–µ –Љ–љ–Њ–ґ–Є—В–µ–ї–Є. –Я–Њ—Б–ї–µ —Н—В–Њ–≥–Њ —Г–Љ–љ–Њ–ґ–∞—О—В —З–Є—Б–ї–Є—В–µ–ї—М –Є –Ј–љ–∞–Љ–µ–љ–∞—В–µ–ї—М –Ї–∞–ґ–і–Њ–є –і—А–Њ–±–Є –љ–∞ –і–Њ–њ–Њ–ї–љ–Є—В–µ–ї—М–љ—Л–є –Љ–љ–Њ–ґ–Є—В–µ–ї—М.
–£–Љ–љ–Њ–ґ–∞—В—М –Ј–љ–∞–Љ–µ–љ–∞—В–µ–ї—М –Њ–±–µ–Є—Е –і—А–Њ–±–µ–є –љ–µ –Њ–±—П–Ј–∞—В–µ–ї—М–љ–Њ, –≤–µ–і—М –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ –≤ –Њ–±–Њ–Є—Е —Б–ї—Г—З–∞—П—Е –Њ–і–Є–љ–∞–Ї–Њ–≤–Њ, –љ–Њ, –ґ–µ–ї–∞—В–µ–ї—М–љ–Њ, —З—В–Њ–±—Л —Г—З–∞—Й–Є–µ—Б—П —Г–Љ–љ–Њ–ґ–∞–ї–Є –Њ–±–∞ –Ј–љ–∞–Љ–µ–љ–∞—В–µ–ї—П –љ–∞ –і–Њ–њ–Њ–ї–љ–Є—В–µ–ї—М–љ—Л–µ –Љ–љ–Њ–ґ–Є—В–µ–ї–Є –≤ –Ї–∞—З–µ—Б—В–≤–µ –њ—А–Њ–≤–µ—А–Ї–Є вАФ –µ—Б–ї–Є –њ–Њ–ї—Г—З–Є–ї–Њ—Б—М –Њ–і–љ–Њ –Є —В–Њ –ґ–µ —З–Є—Б–ї–Њ вАФ –Ј–љ–∞—З–Є—В –≤—Л—З–Є—Б–ї–µ–љ–Є—П –≤—Л–њ–Њ–ї–љ–µ–љ—Л –њ—А–∞–≤–Є–ї—М–љ–Њ.
–Ґ–∞–Ї–Њ–є –Љ–µ—В–Њ–і –Љ–Њ–ґ–µ—В –њ—А–Є–Љ–µ–љ—П—В—М—Б—П –Є –≤ –њ—А–Њ—Б—В—Л—Е —Б–ї—Г—З–∞—П—Е –њ—А–Є–≤–µ–і–µ–љ–Є—П –Ї –Њ–±—Й–µ–Љ—Г –Ј–љ–∞–Љ–µ–љ–∞—В–µ–ї—О –і—А–Њ–±–љ—Л—Е –≤—Л—А–∞–ґ–µ–љ–Є–є
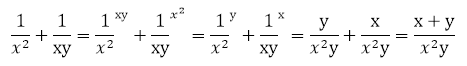
–†–∞–Ј—Г–Љ–µ–µ—В—Б—П, —В–∞–Ї–Њ–є –Љ–µ—В–Њ–і –Њ—В–љ—О–і—М –љ–µ —Б–∞–Љ—Л–є —А–∞—Ж–Є–Њ–љ–∞–ї—М–љ—Л–є, –љ–Њ, –і–ї—П —Г—З–∞—Й–Є—Е—Б—П, –Ї–Њ—В–Њ—А—Л–µ —Б —В—А—Г–і–Њ–Љ –њ–Њ–љ–Є–Љ–∞—О—В –Љ–љ–Њ–≥–Є–µ —В–µ–Љ—Л –Њ–љ –њ–Њ—А–Њ–є –≤–њ–Њ–ї–љ–µ –њ–Њ–і—Е–Њ–і–Є—В.









