–°—А–Њ—З–љ–∞—П –њ—Г–±–ї–Є–Ї–∞—Ж–Є—П –љ–∞—Г—З–љ–Њ–є —Б—В–∞—В—М–Є
+7 995 770 98 40
+7 995 202 54 42
info@journalpro.ru
–Ъ—А–∞–µ–≤–∞—П –Ј–∞–і–∞—З–∞ –і–ї—П —Г—А–∞–≤–љ–µ–љ–Є—П –≥–Є–њ–µ—А–±–Њ–ї–Њ-–њ–∞—А–∞–±–Њ–ї–Є—З–µ—Б–Ї–Њ–≥–Њ —В–Є–њ–∞ —З–µ—В–≤–µ—А—В–Њ–≥–Њ –њ–Њ—А—П–і–Ї–∞
–†—Г–±—А–Є–Ї–∞: –§–Є–Ј–Є–Ї–Њ-–Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–µ –љ–∞—Г–Ї–Є
–Ц—Г—А–љ–∞–ї: «–Х–≤—А–∞–Ј–Є–є—Б–Ї–Є–є –Э–∞—Г—З–љ—Л–є –Ц—Г—А–љ–∞–ї вДЦ4 2018» (–∞–њ—А–µ–ї—М, 2018)
–Ъ–Њ–ї–Є—З–µ—Б—В–≤–Њ –њ—А–Њ—Б–Љ–Њ—В—А–Њ–≤ —Б—В–∞—В—М–Є: 3060
–Я–Њ–Ї–∞–Ј–∞—В—М PDF –≤–µ—А—Б–Є—О –Ъ—А–∞–µ–≤–∞—П –Ј–∞–і–∞—З–∞ –і–ї—П —Г—А–∞–≤–љ–µ–љ–Є—П –≥–Є–њ–µ—А–±–Њ–ї–Њ-–њ–∞—А–∞–±–Њ–ї–Є—З–µ—Б–Ї–Њ–≥–Њ —В–Є–њ–∞ —З–µ—В–≤–µ—А—В–Њ–≥–Њ –њ–Њ—А—П–і–Ї–∞
–Р. –Ь. –®—Е–∞–≥–∞–њ—Б–Њ–µ–≤
–§–У–С–Э–£ ¬Ђ–Ш–љ—Б—В–Є—В—Г—В –њ—А–Є–Ї–ї–∞–і–љ–Њ–є –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Є –Є –∞–≤—В–Њ–Љ–∞—В–Є–Ј–∞—Ж–Є–Є¬ї
360000, –Ъ–С–†, –≥. –Э–∞–ї—М—З–Є–Ї, —Г–ї. –®–Њ—А—В–∞–љ–Њ–≤–∞, 89-–∞
E-mail: ipma@niipma.ru
–Р–љ–љ–Њ—В–∞—Ж–Є—П: –†–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ—В—Б—П –Ї—А–∞–µ–≤–∞—П –Ј–∞–і–∞—З–∞ –і–ї—П —Г—А–∞–≤–љ–µ–љ–Є—П —Б–Љ–µ—И–∞–љ–љ–Њ–≥–Њ –≥–Є–њ–µ—А–±–Њ–ї–Њ-–њ–∞—А–∞–±–Њ–ї–Є—З–µ—Б–Ї–Њ–≥–Њ —В–Є–њ–∞ —З–µ—В–≤–µ—А—В–Њ–≥–Њ –њ–Њ—А—П–і–Ї–∞. –Т –≥–Є–њ–µ—А–±–Њ–ї–Є—З–µ—Б–Ї–Њ–є —З–∞—Б—В–Є –љ–∞–є–і–µ–љ–Њ —А–µ—И–µ–љ–Є–µ –≤ —П–≤–љ–Њ–Љ –≤–Є–і–µ, –∞ –≤ –њ–∞—А–∞–±–Њ–ї–Є—З–µ—Б–Ї–Њ–є —З–∞—Б—В–Є —А–µ—И–µ–љ–Є–µ —Г—А–∞–≤–љ–µ–љ–Є—П –≤—Л–њ–Є—Б—Л–≤–∞–µ—В—Б—П —Б –њ–Њ–Љ–Њ—Й—М—О —Д—Г–љ–Ї—Ж–Є–Є –У—А–Є–љ–∞ –њ–µ—А–≤–Њ–є –Ї—А–∞–µ–≤–Њ–є –Ј–∞–і–∞—З–Є. –Т –ї–Є–љ–Є–Є —Б–Њ–њ—А–Є–Ї–Њ—Б–љ–Њ–≤–µ–љ–Є—П y=0 –њ–Њ–ї—Г—З–µ–љ–Њ –Њ–±—Л–Ї–љ–Њ–≤–µ–љ–љ–∞—П –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–∞—П —Г—А–∞–≤–љ–µ–љ–Є—П —В—А–µ—В—М–µ–≥–Њ –њ–Њ—А—П–і–Ї–∞, —А–µ—И–∞—П –Ї–Њ—В–Њ—А–Њ–≥–Њ –њ–Њ–ї—Г—З–∞–µ–Љ –≥—А–∞–љ–Є—З–љ–Њ–µ —Г—Б–ї–Њ–≤–Є–µ —Г—Б—В—А–∞–љ—П—О—Й–µ–µ –љ–µ–Ї–Њ—А—А–µ–Ї—В–љ–Њ—Б—В—М –Ј–∞–і–∞—З–Є.
–Ъ–ї—О—З–µ–≤—Л–µ —Б–ї–Њ–≤–∞: –£—А–∞–≤–љ–µ–љ–Є—П —Б–Љ–µ—И–∞–љ–љ–Њ–≥–Њ —В–Є–њ–∞ —З–µ—В–≤–µ—А—В–Њ–≥–Њ –њ–Њ—А—П–і–Ї–∞; –ї–Њ–Ї–∞–ї—М–љ–∞—П –Ї—А–∞–µ–≤–∞—П –Ј–∞–і–∞—З–∞; –ї–Є–љ–µ–∞—А–Є–Ј–Њ–≤–∞–љ–љ–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ –Ъ–Њ—А—В–µ–≤–µ–≥–∞-–і–µ-–§—А–Є–Ј–∞; —Д—Г–љ–Ї—Ж–Є—П –У—А–Є–љ–∞.
–Т –љ–∞—Б—В–Њ—П—Й–µ–µ –≤—А–µ–Љ—П —В–µ–Њ—А–Є—П –Ї—А–∞–µ–≤—Л—Е –Ј–∞–і–∞—З –і–ї—П —Г—А–∞–≤–љ–µ–љ–Є–є —Б–Љ–µ—И–∞–љ–љ–Њ–≥–Њ —В–Є–њ–∞ –≤—Л—Б–Њ–Ї–Њ–≥–Њ –њ–Њ—А—П–і–Ї–∞ —П–≤–ї—П–µ—В—Б—П –Њ–і–љ–Є–Љ –Є–Ј –Є–љ—В–µ–љ—Б–Є–≤–љ–Њ —А–∞–Ј–≤–Є–≤–∞—О—Й–Є—Е—Б—П —А–∞–Ј–і–µ–ї–Њ–≤ —Б–Њ–≤—А–µ–Љ–µ–љ–љ–Њ–є —В–µ–Њ—А–Є–Є –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ—Л—Е —Г—А–∞–≤–љ–µ–љ–Є–є —Б —З–∞—Б—В–љ—Л–Љ–Є –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л–Љ–Є. –†–∞–Ј–ї–Є—З–љ—Л–µ –Ї—А–∞–µ–≤—Л–µ –Ј–∞–і–∞—З–Є –і–ї—П —Г—А–∞–≤–љ–µ–љ–Є–є —Б–Љ–µ—И–∞–љ–љ–Њ–≥–Њ —В–Є–њ–∞ –≤—Л—Б–Њ–Ї–Њ–≥–Њ –њ–Њ—А—П–і–Ї–∞ –Є—Б—Б–ї–µ–і–Њ–≤–∞–ї–Є—Б—М –≤ —А–∞–±–Њ—В–∞—Е
–Я—А–Є –Є–Ј—Г—З–µ–љ–Є–Є –≤–Њ–ї–љ –њ–Њ–њ–µ—А–µ—З–љ–Њ–≥–Њ –Ї–Њ–ї–µ–±–∞–љ–Є—П —Б—В–µ—А–ґ–љ—П[4], [5, —Б. 277] –Є–ї–Є –њ—А–Є –Ї–Њ–ї–µ–±–∞–љ–Є–Є –±–∞–ї–Ї–Є [6, —Б. 289] –≤–Њ–Ј–љ–Є–Ї–∞—О—В —А–∞–Ј–ї–Є—З–љ—Л–µ —Г—А–∞–≤–љ–µ–љ–Є—П —З–µ—В–≤–µ—А—В–Њ–≥–Њ –њ–Њ—А—П–і–Ї–∞. –Э–∞ –≤–∞–ґ–љ–Њ—Б—В—М –њ–Њ–і–Њ–±–љ—Л—Е –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є–є –≤ —В–µ–Њ—А–Є–Є —Г—А–∞–≤–љ–µ–љ–Є–є —Б–Љ–µ—И–∞–љ–љ–Њ–≥–Њ —В–Є–њ–∞ —Г–Ї–∞–Ј—Л–≤–∞–ї –Р.–Т. –С–Є—Ж–∞–і–Ј–µ. –Т –Ї–∞—З–µ—Б—В–≤–µ –Љ–Њ–і–µ–ї—М–љ–Њ–≥–Њ —Г—А–∞–≤–љ–µ–љ–Є—П —З–µ—В–≤–µ—А—В–Њ–≥–Њ –њ–Њ—А—П–і–Ї–∞ –Є–Љ –±—Л–ї–Њ –њ—А–µ–і–ї–Њ–ґ–µ–љ–Њ —Г—А–∞–≤–љ–µ–љ–Є–µ [7]:
![]()
–Т –і–∞–љ–љ–Њ–є —А–∞–±–Њ—В–µ —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ—В—Б—П —Г—А–∞–≤–љ–µ–љ–Є–µ
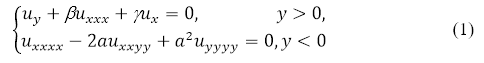
–≤ –Ї–Њ–љ–µ—З–љ–Њ–є –Њ–±–ї–∞—Б—В–Є![]() D2 вАФ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї —Б –≤–µ—А—И–Є–љ–∞–Љ–Є
D2 вАФ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї —Б –≤–µ—А—И–Є–љ–∞–Љ–Є
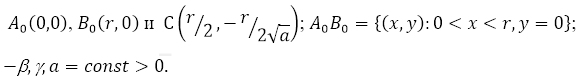
–Ю–њ—А–µ–і–µ–ї–µ–љ–Є–µ. –†–µ–≥—Г–ї—П—А–љ—Л–Љ —А–µ—И–µ–љ–Є–µ–Љ —Г—А–∞–≤–љ–µ–љ–Є—П (1) –≤ –Њ–±–ї–∞—Б—В–Є D –љ–∞–Ј–Њ–≤–µ–Љ —Д—Г–љ–Ї—Ж–Є—О![]() —Г–і–Њ–≤–ї–µ—В–≤–Њ—А—П—О—Й—Г—О —Г—А–∞–≤–љ–µ–љ–Є—О (1).
—Г–і–Њ–≤–ї–µ—В–≤–Њ—А—П—О—Й—Г—О —Г—А–∞–≤–љ–µ–љ–Є—О (1).
–Ч–∞–і–∞—З–∞. –Э–∞–є—В–Є —А–µ–≥—Г–ї—П—А–љ–Њ–µ –≤ –Њ–±–ї–∞—Б—В–Є D —А–µ—И–µ–љ–Є–µ![]() —Г—А–∞–≤–љ–µ–љ–Є—П (1), —Г–і–Њ–≤–ї–µ—В–≤–Њ—А—П—О—Й–µ–µ —Б–ї–µ–і—Г—О—Й–Є–Љ –Ї—А–∞–µ–≤—Л–Љ —Г—Б–ї–Њ–≤–Є—П–Љ:
—Г—А–∞–≤–љ–µ–љ–Є—П (1), —Г–і–Њ–≤–ї–µ—В–≤–Њ—А—П—О—Й–µ–µ —Б–ї–µ–і—Г—О—Й–Є–Љ –Ї—А–∞–µ–≤—Л–Љ —Г—Б–ї–Њ–≤–Є—П–Љ:
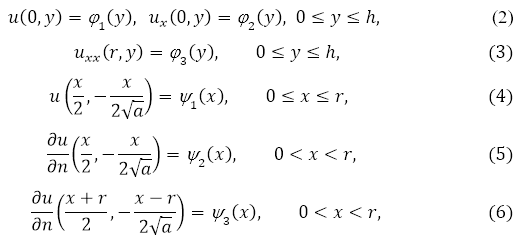
–≥–і–µ n вАФ –≤–љ—Г—В—А–µ–љ–љ—П—П –љ–Њ—А–Љ–∞–ї—М;![]() вАФ –Ј–∞–і–∞–љ–љ—Л–µ —Д—Г–љ–Ї—Ж–Є–Є –Є –≤—Л–њ–Њ–ї–љ—П—О—В—Б—П —Г—Б–ї–Њ–≤–Є—П —Б–Њ–≥–ї–∞—Б–Њ–≤–∞–љ–Є—П:
вАФ –Ј–∞–і–∞–љ–љ—Л–µ —Д—Г–љ–Ї—Ж–Є–Є –Є –≤—Л–њ–Њ–ї–љ—П—О—В—Б—П —Г—Б–ї–Њ–≤–Є—П —Б–Њ–≥–ї–∞—Б–Њ–≤–∞–љ–Є—П:![]()
–£—А–∞–≤–љ–µ–љ–Є–µ (1) –≤ –Њ–±–ї–∞—Б—В–Є D2 –Љ–Њ–ґ–љ–Њ —Б–≤–µ—Б—В–Є –Ї —Б–Є—Б—В–µ–Љ–µ —Г—А–∞–≤–љ–µ–љ–Є–є
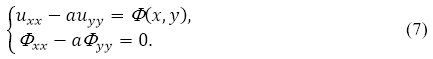
–Ш–Ј –Ї—А–∞–µ–≤—Л—Е —Г—Б–ї–Њ–≤–Є–є (5) –Є (6) –і–ї—П –§(x,y) –њ–Њ–ї—Г—З–∞–µ–Љ —Б–ї–µ–і—Г—О—Й–µ–µ:
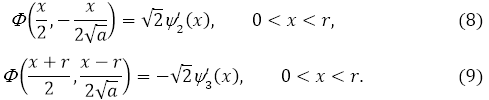
–†–µ—И–µ–љ–Є–µ –Ј–∞–і–∞—З–Є –У—Г—А—Б–∞ (8), (9) –і–ї—П —Г—А–∞–≤–љ–µ–љ–Є—П
![]()
–Є–Љ–µ–µ—В –≤–Є–і
![]()
–Ш–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ —А–µ—И–µ–љ–Є–µ —Г—А–∞–≤–љ–µ–љ–Є—П
![]()
–њ—А–µ–і—Б—В–∞–≤–Є–Љ–Њ –≤ –≤–Є–і–µ:
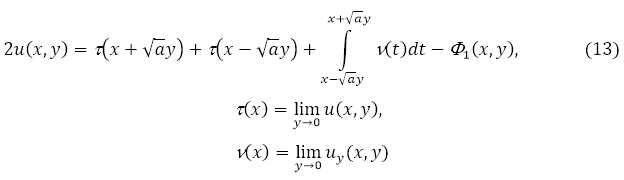
вАФ –њ–Њ–Ї–∞ –љ–µ–Є–Ј–≤–µ—Б—В–љ—Л–µ —Д—Г–љ–Ї—Ж–Є–Є, –∞
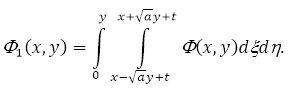
–Ш—Б–њ–Њ–ї—М–Ј—Г—П —Г—Б–ї–Њ–≤–Є–µ (4), –Є–Ј (10) –њ–Њ–ї—Г—З–Є–Љ —Б–ї–µ–і—Г—О—Й–µ–µ —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ –Љ–µ–ґ–і—Г ![]()
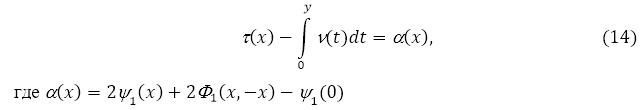
вАФ –Є–Ј–≤–µ—Б—В–љ–∞—П —Д—Г–љ–Ї—Ж–Є—П.
–Т –Њ–±–ї–∞—Б—В–Є D1 –њ–µ—А–µ—Е–Њ–і—П –Ї –њ—А–µ–і–µ–ї—Г y вЖТ 0 –≤ —Г—А–∞–≤–љ–µ–љ–Є–Є (1), –њ–Њ–ї—Г—З–Є–Љ —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ –Љ–µ–ґ–і—Г ![]() –≤ –≤–Є–і–µ
–≤ –≤–Є–і–µ
![]()
–†–µ—И–∞—П —Б–Є—Б—В–µ–Љ—Г —Г—А–∞–≤–љ–µ–љ–Є–є (14) –Є (15) –њ—А–Є—Е–Њ–і–Є–Љ –Ї –Њ–±—Л–Ї–љ–Њ–≤–µ–љ–љ–Њ–Љ—Г –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–Љ—Г —Г—А–∞–≤–љ–µ–љ–Є—О
![]()
—Б –≥—А–∞–љ–Є—З–љ—Л–Љ–Є —Г—Б–ї–Њ–≤–Є—П–Љ–Є
![]()
–° –њ–Њ–Љ–Њ—Й—М—О —Г—Б–ї–Њ–≤–Є–є (17) —Г—А–∞–≤–љ–µ–љ–Є–µ (16) —Б–≤–Њ–і–Є—В—Б—П –Ї –Є–љ—В–µ–≥—А–∞–ї—М–љ–Њ–Љ—Г —Г—А–∞–≤–љ–µ–љ–Є—О
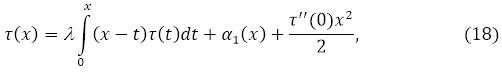
–≥–і–µ 
–Ю–±—А–∞—Й–∞—П –Є–љ—В–µ–≥—А–∞–ї—М–љ–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ (18) –Є—Б–њ–Њ–ї—М–Ј—Г—П —Г—Б–ї–Њ–≤–Є–µ (17) –Є–Љ–µ–µ–Љ
![]()
–≥–і–µ
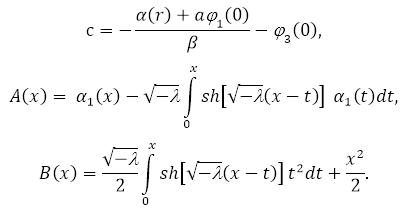
–Ф–∞–ї–µ–µ —А–∞—Б—Б–Љ–Њ—В—А–Є–Љ —Г—А–∞–≤–љ–µ–љ–Є–µ (1) –≤ –њ–∞—А–∞–±–Њ–ї–Є—З–µ—Б–Ї–Њ–є —З–∞—Б—В–Є.
–Ч–∞–Љ–µ–љ–∞ —Д—Г–љ–Ї—Ж–Є–Є ![]() , –≥–і–µ N = const –≤ —Г—А–∞–≤–љ–µ–љ–Є–Є (1) –њ—А–Є y > 0 –њ—А–Є–≤–Њ–і–Є—В –Ї —Б–ї–µ–і—Г—О—Й–µ–Љ—Г –≤–Є–і—Г
, –≥–і–µ N = const –≤ —Г—А–∞–≤–љ–µ–љ–Є–Є (1) –њ—А–Є y > 0 –њ—А–Є–≤–Њ–і–Є—В –Ї —Б–ї–µ–і—Г—О—Й–µ–Љ—Г –≤–Є–і—Г
![]()
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В–Њ–ґ–і–µ—Б—В–≤–Њ
![]()
–Я—А–Њ–і–µ–ї–∞–≤ –љ–µ–Ї–Њ—В–Њ—А—Л–µ –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П –Є–Ј (21) –њ–Њ–ї—Г—З–Є–Љ
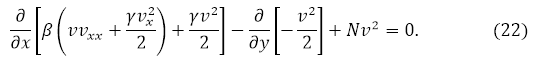
–Ш–љ—В–µ–≥—А–Є—А—Г—П (22) –њ–Њ –Њ–±–ї–∞—Б—В–Є
![]()
–Є –њ—А–Є–Љ–µ–љ—П—П, —Д–Њ—А–Љ—Г–ї—Г –У—А–Є–љ–∞ –њ–Њ–ї—Г—З–∞–µ–Љ
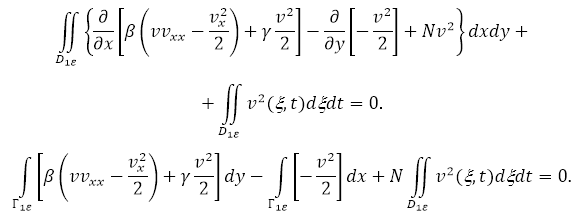
–≥–і–µ ![]() –≥—А–∞–љ–Є—Ж–∞ –Њ–±–ї–∞—Б—В–Є
–≥—А–∞–љ–Є—Ж–∞ –Њ–±–ї–∞—Б—В–Є ![]()
–Я–µ—А–µ—Е–Њ–і—П –Ї –њ—А–µ–і–µ–ї—Г –њ—А–Є ![]() –њ–µ—А–µ–њ–Є—И–µ–Љ –њ–Њ—Б–ї–µ–і–љ–µ–µ –≤ –≤–Є–і–µ
–њ–µ—А–µ–њ–Є—И–µ–Љ –њ–Њ—Б–ї–µ–і–љ–µ–µ –≤ –≤–Є–і–µ

–£—З–Є—В—Л–≤–∞—П –Њ–і–љ–Њ—А–Њ–і–љ–Њ—Б—В—М —Г—Б–ї–Њ–≤–Є–є (2), (13) –Є (18) –њ–Њ–ї—Г—З–∞–µ–Љ —Б–ї–µ–і—Г—О—Й–µ–µ —А–∞–≤–µ–љ—Б—В–≤–Њ –≤ –≤–Є–і–µ
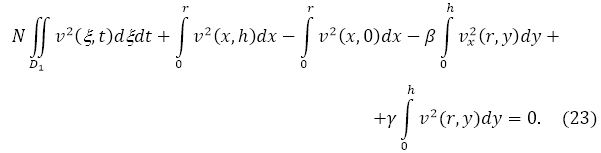
–Ф–Њ–Ї–∞–ґ–µ–Љ —Б–љ–∞—З–∞–ї–∞, —З—В–Њ ![]() –µ—Б–ї–Є
–µ—Б–ї–Є ![]()
–Ю–±—Й–µ–µ —А–µ—И–µ–љ–Є–µ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–µ–≥–Њ –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–≥–Њ —Г—А–∞–≤–љ–µ–љ–Є—П (16) –Є–Љ–µ–µ—В –≤–Є–і
![]()
–Я–Њ–і—Б—В–∞–≤–ї—П—П –Њ–і–љ–Њ—А–Њ–і–љ—Л–µ –≥—А–∞–љ–Є—З–љ—Л–µ —Г—Б–ї–Њ–≤–Є—П –≤ –Њ–±—Й–µ–µ —А–µ—И–µ–љ–Є–µ, –њ–Њ–ї—Г—З–Є–Љ —Б–Є—Б—В–µ–Љ—Г –∞–ї–≥–µ–±—А–∞–Є—З–µ—Б–Ї–Є—Е —Г—А–∞–≤–љ–µ–љ–Є–є –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ –њ—А–Њ–Є–Ј–≤–Њ–ї—М–љ—Л—Е –њ–Њ—Б—В–Њ—П–љ–љ—Л—Е C1, C2 , C3 –≤ –≤–Є–і–µ
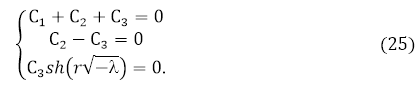
–†–µ—И–∞—П —Б–Є—Б—В–µ–Љ—Г (25), –љ–∞—Е–Њ–і–Є–Љ ![]() . –° —Г—З–µ—В–Њ–Љ —Н—В–Њ–≥–Њ, –≤—Л—А–∞–ґ–µ–љ–Є–µ (23) –њ—А–Є–Љ–µ—В –≤–Є–і
. –° —Г—З–µ—В–Њ–Љ —Н—В–Њ–≥–Њ, –≤—Л—А–∞–ґ–µ–љ–Є–µ (23) –њ—А–Є–Љ–µ—В –≤–Є–і
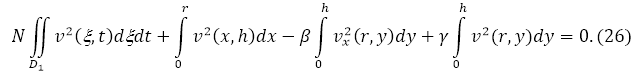
–І–Є—Б–ї–Њ N –≤—Л–±–Є—А–∞–µ–Љ —В–∞–Ї, —З—В–Њ –±—Л –ї–µ–≤–∞—П —З–∞—Б—В—М —Г—А–∞–≤–љ–µ–љ–Є—П (26) —Б—В–∞–ї–Њ –±–Њ–ї—М—И–µ –ї–Є–±–Њ —А–∞–≤–љ–Њ –љ—Г–ї—П. –Ґ–Њ–≥–і–∞ –њ—А–Є ![]() —Б–ї–µ–і—Г–µ—В, —З—В–Њ
—Б–ї–µ–і—Г–µ—В, —З—В–Њ ![]()
–Ш–Ј —Н—В–Њ–≥–Њ —Б–ї–µ–і—Г–µ—В, —З—В–Њ –Є—Б—Е–Њ–і–љ–∞—П –Ј–∞–і–∞—З–∞ –љ–µ –Љ–Њ–ґ–µ—В –Є–Љ–µ—В—М –±–Њ–ї–µ–µ –Њ–і–љ–Њ–≥–Њ —А–µ—И–µ–љ–Є—П –≤ –Њ–±–ї–∞—Б—В–Є D1 –Є —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ –≤ –Њ–±–ї–∞—Б—В–Є D
–Ґ–µ–њ–µ—А—М –њ–µ—А–µ–є–і–µ–Љ –љ–µ–њ–Њ—Б—А–µ–і—Б—В–≤–µ–љ–љ–Њ –Ї –љ–∞—Е–Њ–ґ–і–µ–љ–Є—О —А–µ—И–µ–љ–Є—П –≤ –Њ–±–ї–∞—Б—В–Є D1.
–° –њ–Њ–Љ–Њ—Й—М—О –Ј–∞–Љ–µ–љ—Л –њ–µ—А–µ–Љ–µ–љ–љ–Њ–є

—Г—А–∞–≤–љ–µ–љ–Є–µ (1) –≤ –Њ–±–ї–∞—Б—В–Є D1 –Љ–Њ–ґ–љ–Њ —Б–≤–µ—Б—В–Є –Ї –±–Њ–ї–µ–µ –Є–Ј–≤–µ—Б—В–љ–Њ–Љ—Г —Г—А–∞–≤–љ–µ–љ–Є—О
![]()
—А–∞—Б—Б–Љ–Њ—В—А–µ–љ–љ–Њ–µ –≤ –Љ–Њ–љ–Њ–≥—А–∞—Д–Є–Є [8].
–Ы–Є—В–µ—А–∞—В—Г—А–∞
- –Х–ї–µ–µ–≤ –Т.–Р. –Ъ—А–∞–µ–≤—Л–µ –Ј–∞–і–∞—З–Є –і–ї—П —Б–Љ–µ—И–∞–љ–љ–Њ–≥–Њ —Г—А–∞–≤–љ–µ–љ–Є—П –≥–Є–њ–µ—А–±–Њ–ї–Њ-–њ–∞—А–∞–±–Њ–ї–Є—З–µ—Б–Ї–Њ–≥–Њ —В–Є–њ–∞ —В—А–µ—В—М–µ–≥–Њ –њ–Њ—А—П–і–Ї–∞ // –Э–µ–ї–Є–љ–µ–є–љ—Л–µ —Н–≤–Њ–ї—О—Ж–Є–Њ–љ–љ—Л–µ —Г—А–∞–≤–љ–µ–љ–Є—П –≤ –њ—А–Є–Ї–ї–∞–і–љ–Њ–є –Ј–∞–і–∞—З–µ. –Ъ–Є–µ–≤, 1991. –°. 36 вАФ 38
- –Х–ї–µ–µ–≤ –Т.–Р. –Ю–± –Њ–і–љ–Њ–є –Ј–∞–і–∞—З–µ —Б –љ–µ–ї–Њ–Ї–∞–ї—М–љ—Л–Љ —Б–і–≤–Є–≥–Њ–Љ –і–ї—П —Г—А–∞–≤–љ–µ–љ–Є—П —Б–Љ–µ—И–∞–љ–љ–Њ–≥–Њ —В–Є–њ–∞ —В—А–µ—В—М–µ–≥–Њ –њ–Њ—А—П–і–Ї–∞ // –Ь–∞—В–µ—А–Є–∞–ї—Л –≤—В–Њ—А–Њ–≥–Њ –Ь–µ–ґ–і—Г–љ–∞—А–Њ–і–љ–Њ–≥–Њ –†–Њ—Б—Б–Є–є—Б–Ї–Њ вАФ –Ъ–∞–Ј–∞—Е—Б–Ї–Њ–≥–Њ —Б–Є–Љ–њ–Њ–Ј–Є—Г–Љ–∞ ¬Ђ–£—А–∞–≤–љ–µ–љ–Є—П —Б–Љ–µ—И–∞–љ–љ–Њ–≥–Њ —В–Є–њ–∞ –Є —А–Њ–і—Б—В–≤–µ–љ–љ—Л–µ –њ—А–Њ–±–ї–µ–Љ—Л –∞–љ–∞–ї–Є–Ј–∞ –Є –Є–љ—Д–Њ—А–Љ–∞—В–Є–Ї–Є¬ї. –Э–∞–ї—М—З–Є–Ї, 2011. –°. 69 вАФ 71.
- –Х–ї–µ–µ–≤ –Т. –Р., –Ъ—Г–Љ—Л–Ї–Њ–≤–∞ –°. –Ъ. –Т–љ—Г—В—А–µ–љ–µ–Ї—А–∞–µ–≤–∞—П –Ј–∞–і–∞—З–∞ –і–ї—П —Г—А–∞–≤–љ–µ–љ–Є—П —Б–Љ–µ—И–∞–љ–љ–Њ–≥–Њ —В–Є–њ–∞ —В—А–µ—В—М–µ–≥–Њ –њ–Њ—А—П–і–Ї–∞ —Б –Ї—А–∞—В–љ—Л–Љ–Є —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–∞–Љ–Є // –Ш–Ј–≤–µ—Б—В–Є—П –Ъ–∞–±–∞—А–і–Є–љ–Њ-–С–∞–ї–Ї–∞—А—Б–Ї–Њ–≥–Њ –љ–∞—Г—З–љ–Њ–≥–Њ —Ж–µ–љ—В—А–∞ –†–Р–Э. 2010. вДЦ 5. –°.
5-14. - –Т–Є–љ–Њ–≥—А–∞–і–Њ–≤–∞ –Ь. –Т., –†—Г–і–µ–љ–Ї–Њ –Ю. –Т., –°—Г—Е–Њ—А—Г–Ї–Њ–≤ –Р. –Я. –Ґ–µ–Њ—А–Є—П –≤–Њ–ї–љ. –Ь.: –Э–∞—Г–Ї–∞, 1990. вАФ 432—Б.
- –†–µ–ї–µ–є –Ы. –Р. –Ґ–µ–Њ—А–Є—П –Ј–≤—Г–Ї–∞. –Ь.: –У–Ш–Ґ–Ґ–Ы, 1940. вАФ 499—Б.
- –Ґ–Є–Љ–Њ—И–µ–љ–Ї–Њ –°. –Я. –Ъ–Њ–ї–µ–±–∞–љ–Є—П –≤ –Є–љ–ґ–µ–љ–µ—А–љ–Њ–Љ –і–µ–ї–µ. –Ь.: –У–Ш–§–Ь–Ы, 1959. вАФ 440—Б.
- –С–Є—Ж–∞–і–Ј–µ –Р. –Т. –£—А–∞–≤–љ–µ–љ–Є—П —Б–Љ–µ—И–∞–љ–љ–Њ–≥–Њ —В–Є–њ–∞. –Ь.: –Р–Э –°–°–°–†, 1959. вАФ 164—Б.
- –Ф–ґ—Г—А–∞–µ–≤ –Ґ. –Ф. –Ъ—А–∞–µ–≤—Л–µ –Ј–∞–і–∞—З–Є –і–ї—П —Г—А–∞–≤–љ–µ–љ–Є–є —Б–Љ–µ—И–∞–љ–љ–Њ–≥–Њ –Є —Б–Љ–µ—И–∞–љ–љ–Њ-—Б–Њ—Б—В–∞–≤–љ–Њ–≥–Њ —В–Є–њ–Њ–≤. –Ґ–∞—И–Ї–µ–љ—В: –§–Р–Э, 1979. вАФ 230—Б.









